From Local Concepts to Universals: Evaluating the Multicultural Understanding of Vision-Language Models

Mehar Bhatia, Sahithya Ravi*, Aditya Chinchure*, Eunjeong Hwang, Vered Shwartz
University of British Columbia, Vector Institute of AI
Under review
*Indicates Equal Contribution
Paper (Arxiv) Code Data

Abstract

Despite recent advancements in vision-language models, their performance remains suboptimal on images from non-western cultures due to underrepresentation in training datasets. Various benchmarks have been proposed to test models' cultural inclusivity, but they have limited coverage of cultures and do not adequately assess cultural diversity across universal as well as culture-specific local concepts. To address these limitations, we introduce the GlobalRG benchmark, comprising two challenging tasks: retrieval across universals and cultural visual grounding. The former task entails retrieving culturally diverse images for universal concepts from 50 countries, while the latter aims at grounding culture-specific concepts within images from 15 countries. Our evaluation across a wide range of models reveals that the performance varies significantly across cultures -- underscoring the necessity for enhancing multicultural understanding in vision-language models.

An example instance from each task in GlobalRG benchmark: (i) Retrieval Across Universals measures the ability of VLMs to retrieve culturally diverse images for a query q. (ii) Cultural Visual Grounding aims to evaluate the ability of VLMs to identify a cultural concept q.

Research Questions Discussed

  1. Are able to (TASK 1) retrieve relevant and culturally diverse images for universals AND (TASK2) ground culture-specific local concepts?
  2. Do VLMs exhibit biases towards images from specific cultures?
  3. What are the challenges faced by VLMs in achieving (Task 1) high cultural diversity AND (TASK 2) grounding culture-specific concepts??

Task 1: Retrieval Across Universals


Task Definition

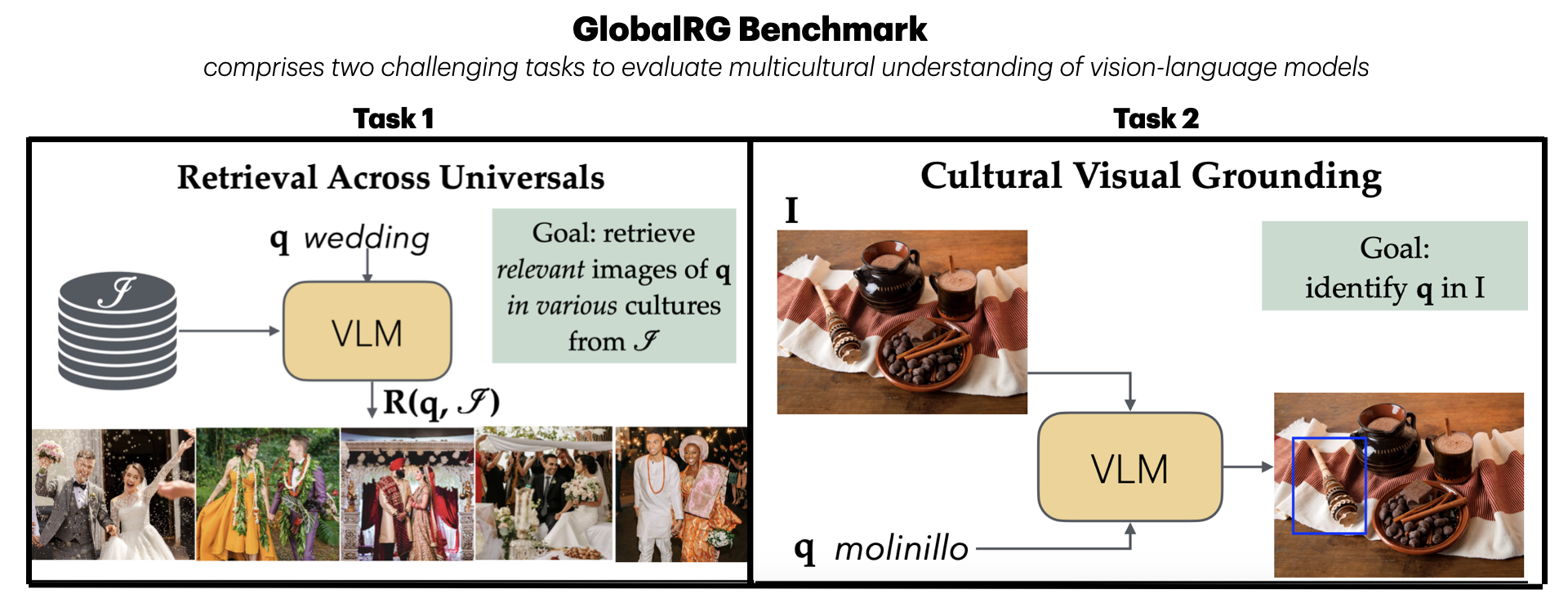
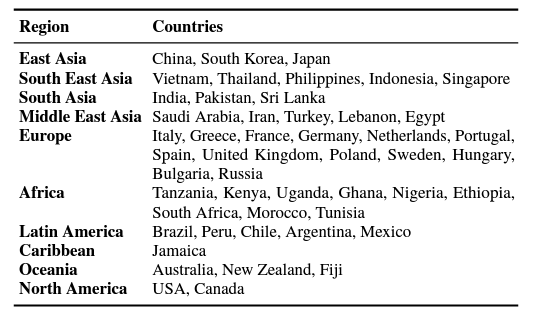
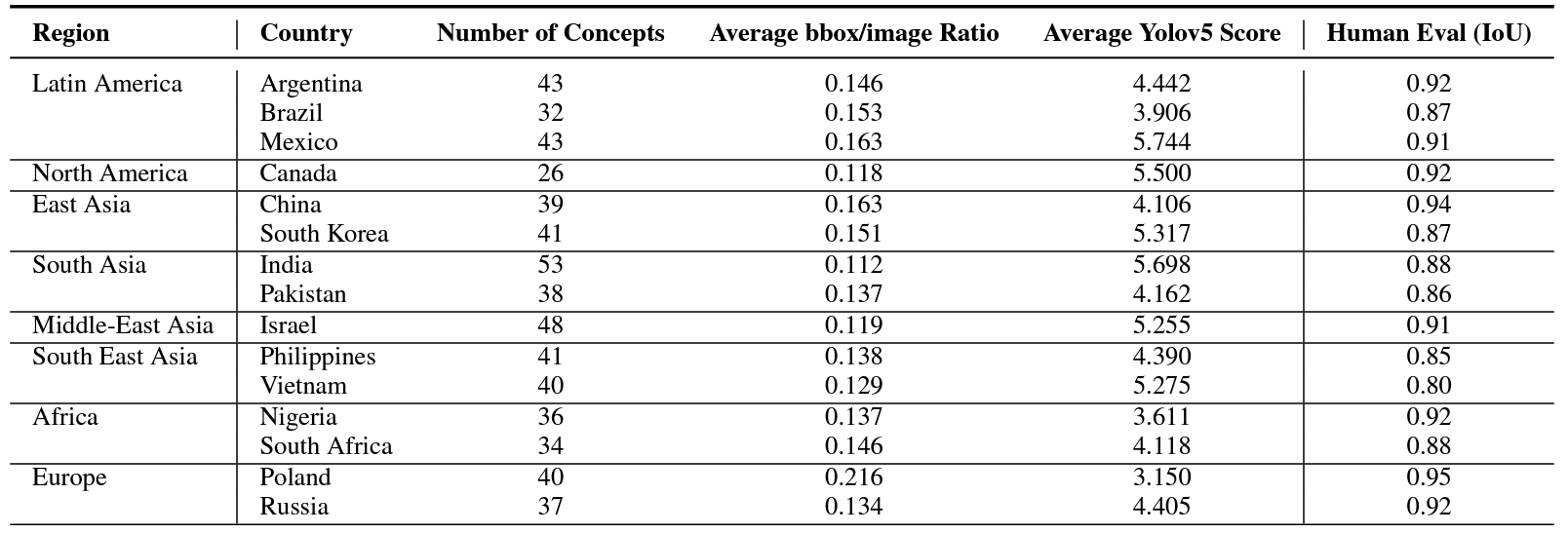
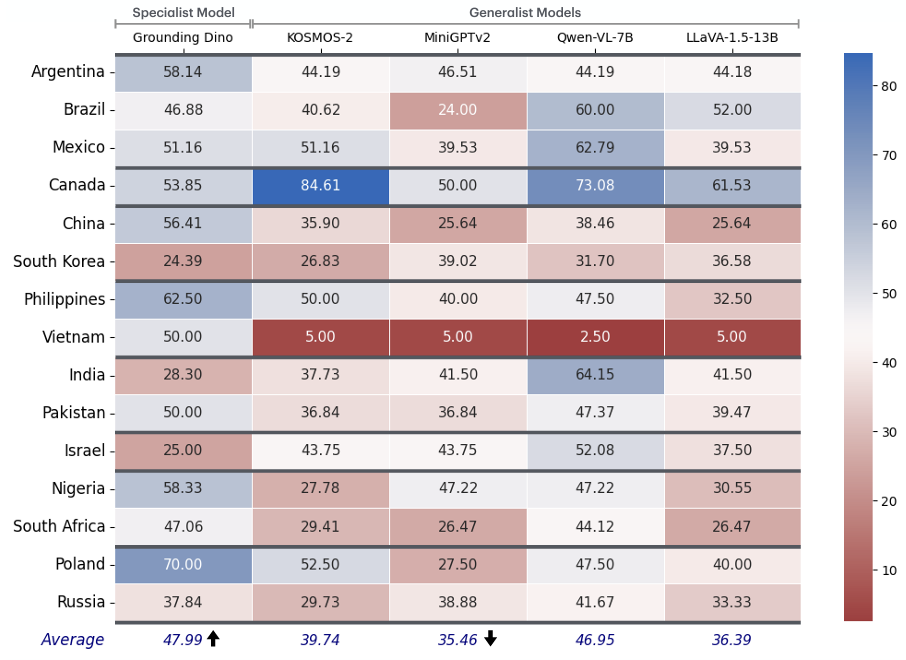
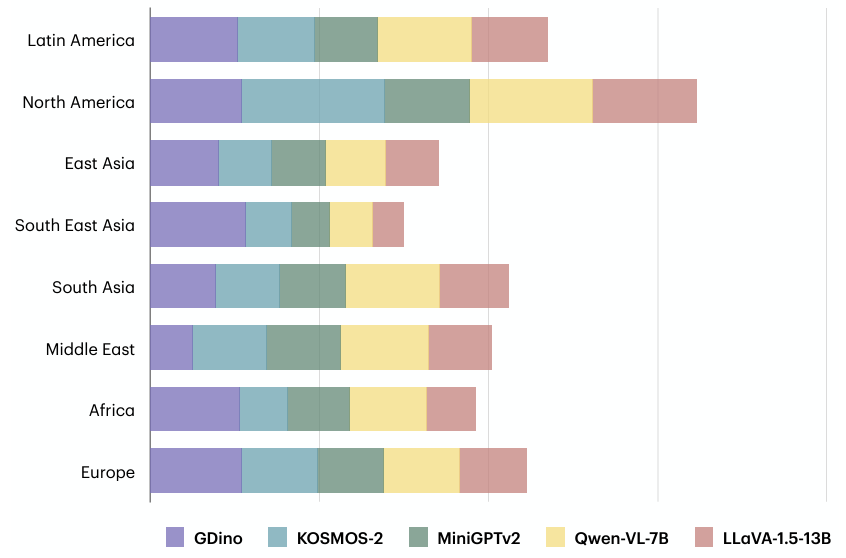
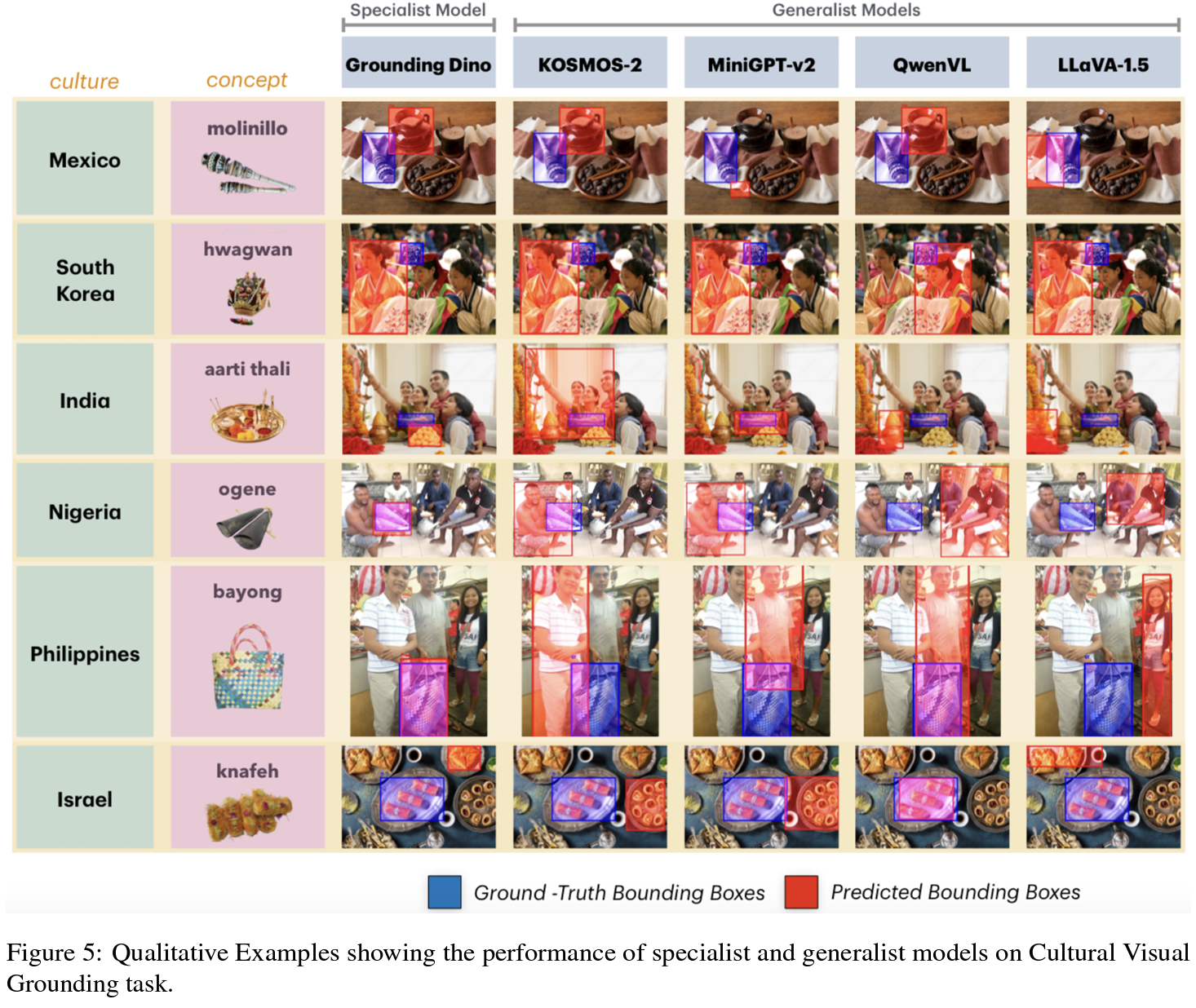
Let \( Q = \{q_1, q_2, \ldots, q_n\} \) be a set of textual queries representing universal concepts, and \( I = \{I_1, I_2, \ldots, I_m\} \) the set of images from different cultures. Given a query \( q \in Q \), the goal is to retrieve a ranked list of images \( R(q, I) = \{I_{r1}, I_{r2}, \ldots, I_{rk} \} \subset I \) that maximizes both relevance and cultural diversity.

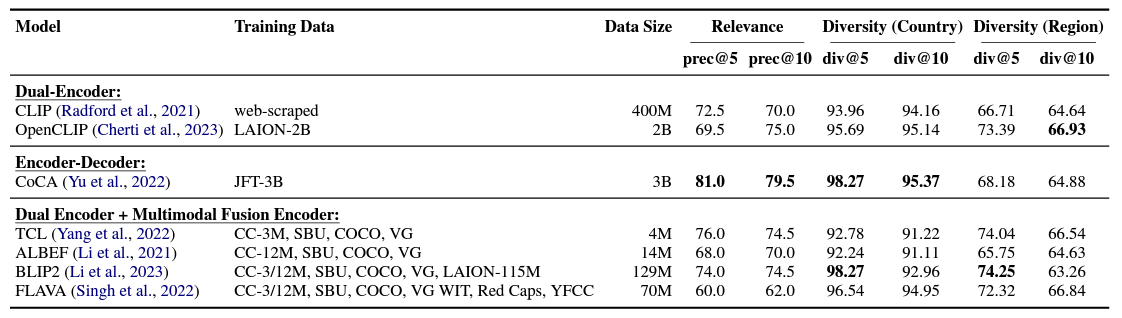
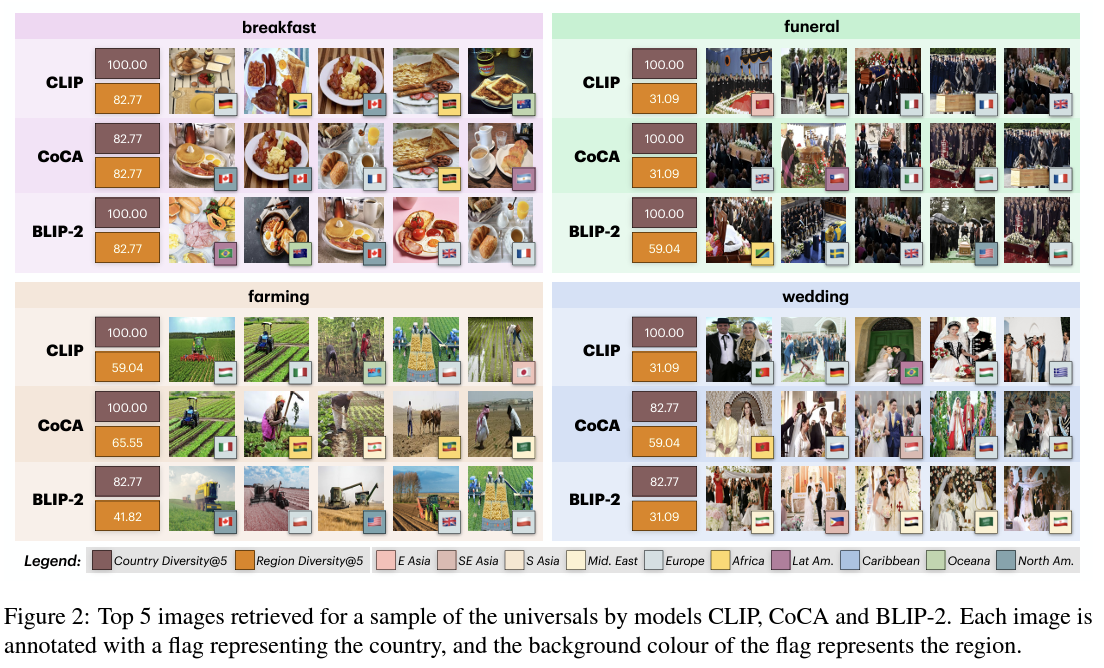
Relevance: \( \text{Rel}(q, I) \) refers to how well the image \( I \) matches the query \( q \) captured by the standard precision@k.
Diversity: \( \text{Div}(R(q, I)) \) measures the cultural diversity of the retrieved images using the formula,

\[ \text{diversity@k} = - \frac{1}{\log m} \sum_{i=1}^{m} p_i \log(p_i) \]

where \( p_i \) is the proportion of images from the \( i \)-th culture in the top \( k \) retrieved images \( R(q) \),
and \( m \) is the total number of cultures in the top \( k \).

A high entropy value (∼ 100) indicates high diversity, retrieved images are well-distributed across different cultures.
Conversely, a low entropy value (∼ 0) indicates low diversity, retrieved images are biased towards specific cultures.


Dataset Statistics

First Image

List of 50 cultures covered in the retrieval task.

Second Image

Human universals used as textual queries in 'Retrieval across Universals' task.



Model Performance

First Image

Average performance of various VLMs on the Retrieval across universals task, in terms of Relevance and Diversity.



Top-5 images retrieved for a sample of universals by models CLIP, CoCA and BLIP-2.

Task 2: Cultural Visual Grounding


Task Definition

Given an image \( I \) and a query \( q \) describing a cultural keyword, the goal is to predict a bounding box \( R \) around the region in \( I \) that corresponds to \( q \). We evaluate models based on the overlap between the gold standard and predicted regions of interest, using Intersection over Union (IoU) as the metric, defined as:

\[ \text{IoU} = \frac{|R \cap R_{\text{gold}}|}{|R \cup R_{\text{gold}}|} \]

where \( R \) is the predicted bounding box and \( R_{\text{gold}} \) is the ground truth bounding box.

We consider a predicted bounding box correct if its IoU with the ground truth bounding box is greater than 0.5, and report overall accuracy.


Dataset Statistics

First Image

Detailed statistics of annotated images across different cultural groups and regions for Cultural Visual Grounding task.



Model Performance

First Image

Country-level Accuracy of each model on Cultural Visual Grounding task.

Second Image

Country group-level Accuracy of eachmodel on Cultural Visual Grounding task.



Examples

First Image

Citation

If you found this work useful in your own research, please consider citing the following:


        @article{bhatia2024local,
          title={From Local Concepts to Universals: Evaluating the Multicultural Understanding of Vision-Language Models},
          author={Bhatia, Mehar and Ravi, Sahithya and Chinchure, Aditya and Hwang, Eunjeong and Shwartz, Vered},
          journal={arXiv preprint arXiv:2407.00263},
          year={2024}
        }